Polynomial Counter: Difference between revisions
(created page) |
(link to ripple carry circuit) |
||
| (15 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The '''polynomial counter''' is the less significant 7 bits of the CIC's program counter. Unlike most program counters which increment by the size of an instruction, the polynomial counter is stepped according to a special formula: | [[File:LFSR poly.png|thumb|7-bit linear-feedback shift register with zero seed]] | ||
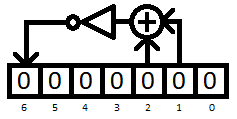
The '''polynomial counter''' is a Fibonacci [https://www.eetimes.com/tutorial-linear-feedback-shift-registers-lfsrs-part-1 linear-feedback shift register] that serves as the less significant 7 bits of the [[CIC]]'s program counter. Its taps are located at bits 1 and 2, which are XOR'd together, inverted, and fed back into bit 6 while the whole register shifts to the right (dividing everything else by two). Unlike most program counters which increment by the size of an instruction, the polynomial counter is stepped according to a special formula: | |||
<pre> | <pre> | ||
void CIC:: | void CIC::poly_inc() | ||
{ | { | ||
bool | // bit 0 is output-only | ||
bool | bool bit1 = pc & 0x01; | ||
bool | bool bit2 = pc & 0x02; | ||
bool bits12_xor = bit1 ^ bit2; | |||
bool bits12_xnor = !bits12_xor; | |||
pc = (pc & 0x380) + ( | pc = (pc & 0x380) + (bits12_xnor * 0x40) + (pc & 0x7E) / 2; | ||
} | } | ||
</pre> | </pre> | ||
Presumably, it takes fewer transistors to step this way than a standard ripple carry incrementor. | Presumably, it takes fewer transistors to step this way than a standard [https://www.falstad.com/circuit/e-counter8.html ripple carry] incrementor. The sum-of-three-terms formula in the pc assignment statement above is equivalent to a bit-shift and bitwise or, which better illuminates the fact that "polynomial" is just a fancy way to describe the linear-feedback: | ||
<pre> | |||
pc = (pc >> 1) | (bits12_xnor * 0x40); | |||
</pre> | |||
If the polynomial counter begins at 00h and runs a straightforward control flow graph (e.g. no jumps/branches/calls/returns), this is the sequence it will count through: | If the polynomial counter begins at 00h and runs a straightforward control flow graph (e.g. no jumps/branches/calls/returns), this is the maximal length sequence with period 127 it will count through: | ||
<pre> | <pre> | ||
| Line 27: | Line 35: | ||
before cycling back to 00h. | before cycling back to 00h. | ||
Note that 7Fh is unique in that it is the only 7-bit value that does not appear in this sequence. That is because 7Fh is idempotent - if the counter ever reaches 7Fh somehow (like through a JMP) then trying to step it will only result in it staying at 7F, so the CIC hangs at that address. | Note that 7Fh is unique in that it is the only 7-bit value that does not appear in this sequence. That is because 7Fh is [https://mathworld.wolfram.com/Idempotent.html idempotent] - if the counter ever reaches 7Fh somehow (like through a JMP) then trying to step it will only result in it staying at 7F, so the CIC hangs at that address. | ||
=== See Also === | |||
* [[S-DSP/Noise]] | |||
'''Sources:''' | |||
* https://problemkaputt.de/fullsnes.htm#snescartridgecicnotes | |||
* https://hackmii.com/2010/01/the-weird-and-wonderful-cic | |||
[[Category:SNES Hardware]] | |||
[[Category:Registers]] | |||
Latest revision as of 00:57, 8 December 2023
The polynomial counter is a Fibonacci linear-feedback shift register that serves as the less significant 7 bits of the CIC's program counter. Its taps are located at bits 1 and 2, which are XOR'd together, inverted, and fed back into bit 6 while the whole register shifts to the right (dividing everything else by two). Unlike most program counters which increment by the size of an instruction, the polynomial counter is stepped according to a special formula:
void CIC::poly_inc()
{
// bit 0 is output-only
bool bit1 = pc & 0x01;
bool bit2 = pc & 0x02;
bool bits12_xor = bit1 ^ bit2;
bool bits12_xnor = !bits12_xor;
pc = (pc & 0x380) + (bits12_xnor * 0x40) + (pc & 0x7E) / 2;
}
Presumably, it takes fewer transistors to step this way than a standard ripple carry incrementor. The sum-of-three-terms formula in the pc assignment statement above is equivalent to a bit-shift and bitwise or, which better illuminates the fact that "polynomial" is just a fancy way to describe the linear-feedback:
pc = (pc >> 1) | (bits12_xnor * 0x40);
If the polynomial counter begins at 00h and runs a straightforward control flow graph (e.g. no jumps/branches/calls/returns), this is the maximal length sequence with period 127 it will count through:
00 40 60 70 78 7c 7e 3f 5f 6f 77 7b 7d 3e 1f 4f 67 73 79 3c 5e 2f 57 6b 75 3a 1d 0e 07 43 61 30 58 6c 76 3b 5d 2e 17 4b 65 32 19 0c 46 23 51 28 54 6a 35 1a 0d 06 03 41 20 50 68 74 7a 3d 1e 0f 47 63 71 38 5c 6e 37 5b 6d 36 1b 4d 26 13 49 24 52 29 14 4a 25 12 09 04 42 21 10 48 64 72 39 1c 4e 27 53 69 34 5a 2d 16 0b 45 22 11 08 44 62 31 18 4c 66 33 59 2c 56 2b 55 2a 15 0a 05 02 01
before cycling back to 00h.
Note that 7Fh is unique in that it is the only 7-bit value that does not appear in this sequence. That is because 7Fh is idempotent - if the counter ever reaches 7Fh somehow (like through a JMP) then trying to step it will only result in it staying at 7F, so the CIC hangs at that address.
See Also
Sources: